انتگرال (به انگلیسی: Integral) مقدار مشترک ممکن زیرینهٔ مجموعه‌ای ریمانی و زبرینهٔ مجموعه‌ای ریمانی یک تابع حقیقی در بازهٔ مفروض است. انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل می‌دهند.

نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.

\int _{{a}}^{{b}}f(x)\,dx

$a$ و $b$ نقاط ابتدا و انتهای بازه هستند و $f(x)$ تابعی انتگرال‌پذیر است و $dx$ نمادی برای متغیر انتگرال‌گیری است.

از لحاظ تاریخی $dx$ یک کمیت بی‌نهایت کوچک را نشان می‌دهد. هر چند در تئوری‌های جدید، انتگرال‌گیری بر پایه متفاوتی پایه‌گذاری شده‌است.

انتگرال نامعین

تعریف: هرگاه معادله دیفرانسیل تابعی معلوم باشد و بخواهیم معادله اصلی تابع را معلوم کنیم این عمل را انتگرال نامعین نامیده و آن را با نماد $\int$ نمایش می‌دهند. به انتگرال نامعین ضد مشتق نیز گفته می‌شود، زیرا عمل انتگرال نامعین گرفتن دقیقاً برعکس عملیات مشتق‌گیری است. بنا به تعریف، نماد $\int {f(x)}.dx$ را انتگرال نامعین نامیده و حاصل آن را تابعی مانند $F(x)+c$ در نظر می‌گیریم هرگاه داشته باشیم:

\int {f(x)}.dx=F(x)+c

در واقع می‌توان چنین بیان کرد:

F'(x)=f(x)\Leftrightarrow \int {f(x)}.dx=F(x)+c

مثال: مقدار انتگرال تابع $f(x)={\sqrt {x}}+2x^{2}-8$ را حساب کنید:

$\int {f(x)}.dx=\int {(x^{\frac {1}{2}}+2x^{2}-8)}.dx=\int {x^{\frac {1}{2}}}.dx+2\int {x^{2}}.dx-8\int {dx}={\frac {2}{3}}x^{\frac {3}{2}}+{\frac {2}{3}}x^{3}-8x+C$

\Rightarrow \int {f(x)}.dx={\frac {2}{3}}x{\sqrt {x}}+{\frac {2}{3}}x^{3}-8x+C

انتگرال معین

نوشتار اصلی: پاد مشتق

بنا به تعریف، نماد $\int _{a}^{b}f(x).dx$ را انتگرال معین نامیده و حاصل آن را به ازای $a<x<b$ عددی به صورت زیر تعریف می‌کنیم:

$\int _{a}^{b}f(x).dx=F(x)|_{a}^{b}=F(b)-F(a)$

$a$ و $b$ به ترتیب، کرانهای بالا و پایین انتگرال نامیده می‌شوند.

تابع انتگرال‌پذیر

اگر تابعی دارای انتگرال باشد به آن انتگرال‌پذیر گویند.

تعبیر هندسی انتگرال

از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.

نکته انتگرال نمودار سه بعدی(انتگرال دوگانه) معرف حجم محصور زیر نمودار است و انتگرال سه‌گانه معرف پارالل زیر نمودار است (غیرقابل تصور).

مثال

انتگرال یک تابع مثبت پیوسته در بازه (۰٬۱۰) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=۱۰ و خم منحنی $f_{x}$ است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال گیری است.

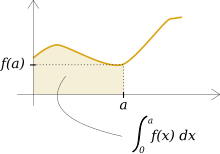
انتگرال یک تابع مساحت زیر نمودار آن تابع است.

انتگرال گیری

(محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است(انتگرال معین). انتگرال را می‌توان عمل برعکس مشتق معرفی نمود(انتگرال نامعین)

مهم‌ترین تعاریف در انتگرال

Integral example with irregular partitions (largest marked in red)

Riemann sums converging

از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لبگ است. انتگرال ریمان به‌وسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه می‌داد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می‌کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال می‌توان به انتگرال ریمان–استیلتیس اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهم‌ترین تعاریف انتگرال می‌باشند:

محاسبه انتگرال

Approximations to integral of √x from 0 to 1, with 5 ■ (yellow) right endpoint partitions and 12 ■ (green) left endpoint partitions

اکثر روش‌های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:

۱٫f تابعی در بازه (a,b) در نظر می‌گیریم. ۲. پاد مشتق f را پیدا می‌کنیم که تابعی است مانند f که و داریم: ۳. قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می‌گیریم:

بنابراین مقدار انتگرال ما برابر خواهد بود.

به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می‌دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار ساده‌ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارت‌اند از:

انتگرال گیری به‌وسیله تغییر متغیر
انتگرال گیری جزء به جزء: $\int u\,dv=uv-\int v\,du$
انتگرال گیری با تغییر متغیر مثلثاتی
انتگرال گیری به‌وسیله تجزیه کسرها

روش‌هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می‌رود همچنین می‌توان بعضی از انتگرال‌ها با ترفندهایی حل کرد برای مثال می‌توانید به انتگرال گاوسی مراجعه کنید.

تقریب انتگرالهای معین

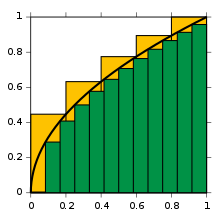
محاسبه سطح زیر نمودار به‌وسیله مستطیل‌هایی زیر نمودار. هر چه قدرعرض مستطیل‌ها کوچک می‌شوندمقدار دقیق تری از مقدار انتگرال بدست می‌آید.

انتگرال‌هایی معین ممکن است با استفاده از روش‌های انتگرال گیری عددی، تخمین زده شوند. یکی از عمومی‌ترین روش‌ها، روش مستطیلی نامیده می‌شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش‌هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه‌ای است. اگر چه روش‌های عددی مقدار دقیق انتگرال را به ما نمی‌دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می‌کند.

کاربرد

انتگرال‌ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک می‌توان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست می‌آید. اما به طور کلی می‌توان آن را تغییرات کمیت حاصل ضرب افقی و عمودی نمودار نامیدمثلا: در یک رابطه کمیت‌ها را تحلیل ابعادی می‌کنیم مثلاً رابطه سرعت و زمان را به صورت زیر نوشته می‌شود:

v=[L]/[T]t=[T]\!

سپس دو تحلیل را در هم ضرب می‌کنیم:

[L]\!

پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.

قسمتی از تدریس استادخلیلی درمحصول مشتق,کاربرد مشتق,مجانب و انتگرال:

اگر فیلم بالا را به صورت آنلاین نمی توانید نگاه کنید نرم افزار adobe flash را از اینجا دانلود و بر روی کامپیوترتان نصب نمایید تا از این به بعد فیلم ها را به صورت آنلاین تماشا کنید

و یا اگر می خواهید این فیلم آموزشی را دانلود کنید و همیشه آن را بر روی کامپیوترتان داشته باشید اینجا کلیک نمایید.

برای تسلط بیشتر روی مبحث انتگرال به شما عزیزان فیلم های آموزشی زیر را توصیه می کنیم:

اطلاعات بیشتر

دیفرانسیل

۲۲۵,۰۰۰ تومان
Select options
اطلاعات بیشتر

مشتق,کاربرد مشتق,مجانب و انتگرال

۱۶۰,۰۰۰ تومان
افزودن به سبد خرید

انتگرال